Trade-off between image resizing, accuracy rate, and prediction time by image recognition

Overview

Currently, I am creating a project to judge the state of image taken by the camera by machine learning. At that time, if the captured image is used as it is, the processing will be heavy and it will take time for learning and judgment, so I decided to make the image rough as a countermeasure.

However, the coarser it is, the lower the recognition accuracy rate will be, so I investigated these trade-offs.

Verification 1: Learning

Resize of image

You can resize the image with opencv's resize () method. The method to read the image file and resize it to the specified scale is as follows.

def fileToImg(file, scale):

 img=cv2.imread(file, cv2.IMREAD_GRAYSCALE)   
 if scale!=1:
    img=cv2.resize(src=img, dsize=(0, 0), fx=scale, fy=scale)
  img=img.astype('float')
  img/=255
  img=img.reshape(img.shape[0], img.shape[1], 1)

 return img

Using this, create training data as follows.

def makeData(scale):
 
  files=glob.glob('*.png')

  datas=[]
  labels=[]

 for i, file in enumerate(files):
 
      img=fileToImg(file, scale)
      datas.append(img)
     
       #Create a label from the file name. Details are omitted.
      label=fileToLabel(file)  
      labels.append(label)
 
  datas=np.array(datas)
  labels=np.array(labels)
  labels=to_categorical(labels)

 return datas, labels

Learning model

The content of the judgment is to classify the image into binary values of 01 according to the content.

A convolutional neural network is used for image recognition. Implementation was done with keras.

def makeModel(input_shape):

  model=tensorflow.keras.models.Sequential()
  model.add(layers.Conv2D(32, (3, 3), activation='relu', 
  input_shape=input_shape))
  model.add(layers.MaxPooling2D((2, 2)))
  model.add(layers.Conv2D(64, (3, 3), activation='relu'))
  model.add(layers.MaxPooling2D((2, 2)))
  model.add(layers.Conv2D(64, (3, 3), activation='relu'))
  model.add(layers.MaxPooling2D((2, 2)))
  model.add(layers.Flatten())
  model.add(layers.Dense(64, activation='relu'))
  model.add(layers.Dense(2, activation='softmax'))

  model.compile(optimizer='adam', loss='categorical_crossentropy', 
  metrics=['accuracy'])

 return model

The accuracy rate is measured as follows.

def getScore(model, x_test, y_test):

  y_pred=model.predict(x_test)
  y_pred_c=np.argmax(y_pred, axis=1)
  y_test_c=np.argmax(y_test, axis=1)

  score=accuracy_score(y_pred_c, y_test_c)
 return score

Measurement of trade-off

Use the following method to check the trade-off between resizing, accuracy rate, and learning time.

def measureScaleEffect(scale):

  datas, labels=makeData(scale)  #make learning data　
 
  x_train, x_test, y_train, y_test=train_test_split(datas, labels,  
  random_state=0)
  model=makeModel(datas[0].shape)　　#make learning model

  start=time.time()  
  model.fit(x_train, y_train, epochs=10, batch_size=32, verbose=0)
  elapsed=time.time()-start  #learning time

  score=getScore(model, x_test, y_test)

 return score, elapsed, model

Result

As a result of performing the above method on various scales, the result is as follows.

Top: Image resizing rate and accuracy rate. Bottom: Image resizing rate and learning time.

By multiplying the image by 0.6 times on each side, I was able to reduce the learning time by about half while maintaining the accuracy rate.

Verification 2: Prediction

However, in reality, I don't really care about the time to learn because I can run it in the middle of the night. More important is the time it takes to predict.

Prediction is required to be real-time, and in some cases it may be necessary to make predictions on a machine with low specifications. (For example, in this project, I will make predictions with raspberry pi)

Therefore, I also tried to verify the trade-off between image resizing and prediction time.

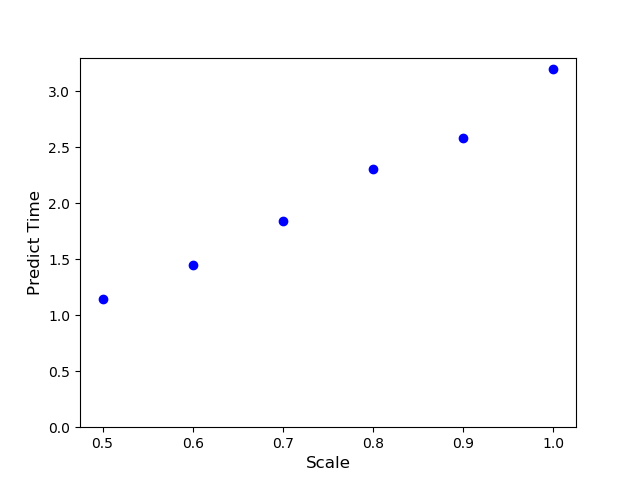
When the resizing rate was set to 0.6, the time required for prediction was also reduced to about half.

Conclusion

By multiplying the image by 0.6 times on one side, the time required for learning and prediction can be halved while maintaining the correct answer rate.

Lastly

I think that the result will change depending on what kind of model you build and what kind of judgment you make, so please use it as a reference.